4 investigadores han propuesto con anterioridad al “Modelo con escaleras de Valturio”, diversas conjeturas con el propósito de modelar Los Artificios de Juanelo.

Don Luis de la Escosura y Morrogh en 1888 y Theodor Beck en 1899 presentan modelos continuos, ambos inspirados en la lámina 95 de “Le diverse et artificiose machine”, Agostino Ramelli, (París 1588).

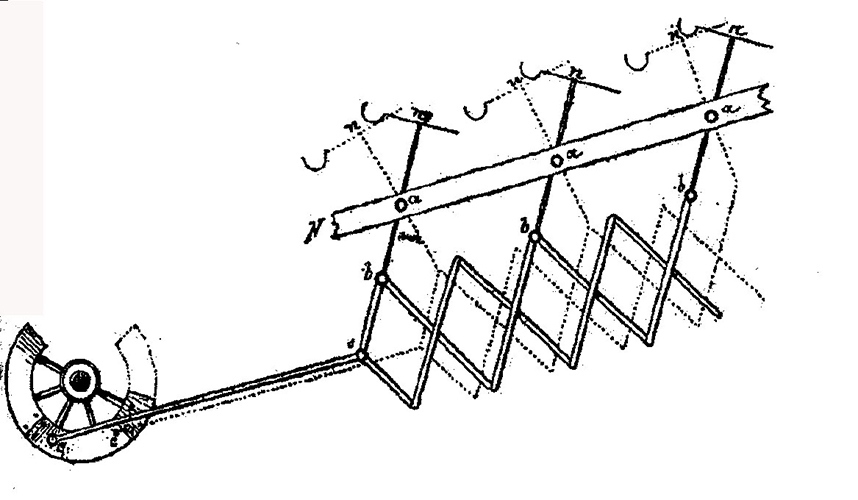
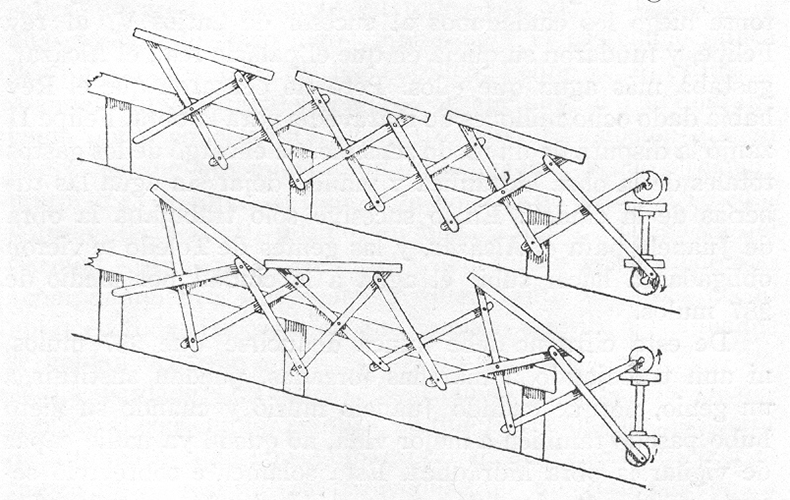
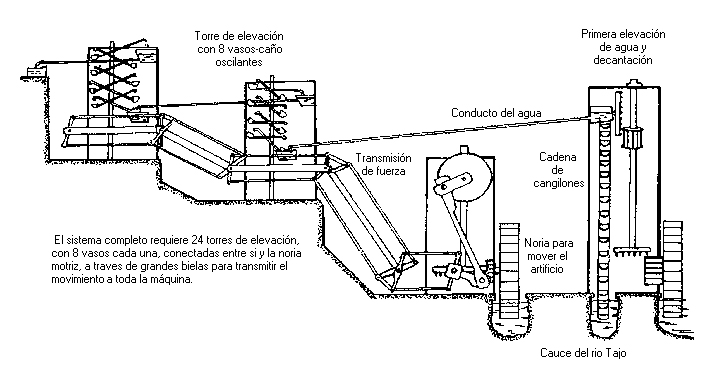
Ladislao Reti propone en 1967, el modelo discontinuo de Torres Oscilantes, formado por torres distantes entre ellas, inspirado en la lámina 96 de “Le diverse et artificiose machine”, Agostino Ramelli, (París 1588). N. García Tapia añadió a posteriori detalles a esta conjetura.

J.L. Peces Ventas, constructor de la maqueta del modelo de Torres Oscilantes expuesta en la Diputación de Toledo, duda durante la construcción de la misma de las soluciones mecánicas usadas, y propone un nuevo modelo contínuo en 1998, del que puede verse una maqueta en el Centro de Interpretación del Toledo Histórico (Toledo).

Las dos primeras conjeturas se descartaron por no poder remontar las fuertes pendientes, que tienen algunos tramos del recorrido de Los Artificios.

El modelo de Torres Oscilantes ha venido siendo el descrito en la bibliografía, aunque varios investigadores y Juanelistas como el propio Peces Ventas o Ángel Moreno Santiago autor del libro “Juanelo y su Artificio. Antología” (2006), detectan y manifiestan dudas razonables, básicamente centradas en la discontinuidad del Artificio, la simplicidad de mecanismos y lagunas referentes a la descripción de Ambrosio de Morales. Recientemente se han introducido variaciones en su definición de elementos constructivos, básicamente referentes a la transmisión de energía, más parecida a la presentada en el “Modelo con escaleras de Valturio”.

La conjetura de J.L. Peces Ventas, aun siendo un elemento continuo no consigue ceñirse a las descripciones existentes, en especial a la de Ambrosio de Morales cuando describe la forma en que se realiza el intercambio del agua, las escaleras de Valturio y las cadencias de los elementos mecánicos.